SOM adalah singkatan dari Self Organizing Maps, dikenal juga dengan nama Kohonen Networks. SOM biasa digunakan dalam kasus unsupervised algorithm, dimana data yang digunakan dalam proses train tidak memiliki label. Dengan kata lain, SOM adalah network yang dapat mengorganisis dirinya sendiri.
Tidak seperti Artificial Neural Network biasanya yang menerapkan konsep error-function evaluation, SOM mengadaptasi konsep competitive learning. Dimana output neurons berkompetisi satu sama lain untuk menjadi pemenang (neuron pemenang akan menjadi neuron yang aktif pada waktu tersebut, untuk setiap iterasi atau setiap waktu hanya akan ada satu output neuron yang menjadi pemenang.
Terdapat empat tahap dalam proses training SOM:
- Initialization
- Sampling
- Matching
- Updating
Pada bagian selanjutnya saya akan menjelaskan satu persatu tahanan training Kohonen Networks, namun sebelum itu saya ingin menjelaskan tentang konsep Topographic Maps pada SOM.
Topographic Maps
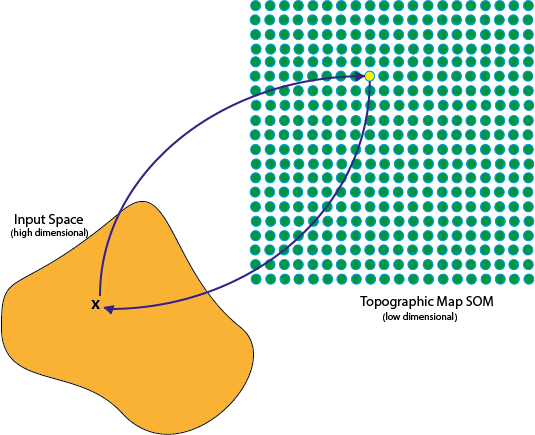
Pada SOM input data akan dimapping kedalam topographic maps, dimana setiap point pada maps mewakili individu pada input data. Konsep topographic maps pada SOM sendiri sebenarnya terinspirasi dari konsep Neurobiological yang menyatakan bahwa setipa input dari sensor (audio, visual, atau yg lain) dipetakan pada suatu lokasi di cerebral cortex. Dikarenakan SOM mengadaptasi konsep formasi topographic maps maka sebuah neuron x dapat berinteraksi dengan neuron disekitarnya, yang mana kekuatan interaksi tersebut akan semakin melemah seiring dengan menjauhnya jarak neuron x dengan neuron yang berinteraksi dengan neuron x.
 |
|---|
| Topographic Maps |
Training Process
Pada bagian ini saya akan menjelaskan tentang proses training Kohonen Networks atau Self Organizing Maps, disini saya akan mengimplementasi proses tersebut menggunakan Python.
Initialization
Dalam tahap ini kita akan melakukan proses randomisasi dalam pemilihan nilai intial untuk weight neuron. Pada SOM input neuron berhubungan langsung dengan output neuron.
Dalam implementasi menggunakan Python, saya menggunakan library numpy yang saya inisialisasi sebagai np. Variable trainData merupakan variable yang merepresentasikan input training data. Sedangkan variable N adalah variable yang merepresentasikan jumlah output neuron pada network.
self.w = np.random.rand(self.N*self.N, train.shape[1])
Penjelasan:
- self.w = weight neuron, self menandakan bahwa variable tersebut adalah bagian dari kelas yang bersangkutan, pada java self memiliki arti yang sama dengan this
- np.random.rand = merupakan fungsi untuk mengenerate nilai random yang berkisar dari 0 hingga 1. Ukuran dari weight adalah row = nilai N * nilai N, column = column data training. Perlu diingat bahwa dimensi untuk setiap vector w sama dengan dimensi sebuah input vector.
Sampling
Pada proses sampling, sebuah datum dari training data akan diambil secara acak. Dalam tahap ini saya tidak mengambil sample data secara acak, akan tetapi secara terurut. Jadi jika ada 50 data, pada proses learning atau iterasi pertama saya kana mengambil data ke 1 menjadi sample. Jadi proses learning akan terjadi sebanyak 50 kali, sesuai dengan jumlah data yang digunakan dalam proses training.
for t, x in enumerate(self.trainData):
Penjalasan:
- t = counter yang menunjukan proses iterasi {0, jumlah training data - 1}
- x = adalah sample yang diambil dari training data untuk setiap proses iterasi
Matching
Pada proses Matching, perhitungan untuk menentukan Best Matching Unit (BMU), weight vector yang memiliki nilai terdekat dengan input vector x. Untuk melakukan proses matching, biasa digunakan Euclidian Distance.
\[dist(x, w_i) = \sqrt{\sum_{h=1}^{n} (w_{ij} - x)^2}\] \[BMU = argmin \| w - x \|\]Perlu diingat bahwa BMU akan direpresentasikan dalam topographic maps. Untuk pengimplementasiannya pada Python
def find_BMU(self, w, x):
dx = np.linalg.norm(w - x, axis=1)
bmu = np.argmin(dx)
return np.unravel_index(bmu, (self.N, self.N))
Penjelasan:
- def find_BMU(self, w, x) = pendefinisian fungsi BMU dengan required parameter w dan w
- dx = np.linalg.norm(w - x, axis=1) = menghitung jarak antra input vector x dengan seluruh weight vector menggunakan Euclidian Distance(axis = 1, menandakan bahwa perhitungan dilakukan sepanjang axis = 1, dalam kasus ini row)
- bmu = np.argmin(dx) = temukan posisi weight vector yang memiliki jarak terdekat dengan input vector.
- np.unravel_index(bmu, (self.N, self.N)) = tentukan posisi bmu pada topographic maps yang berdimensi N * N
Updating
Sebelum proses updating weight neuron, hal yang peratama harus dilakukan adalah menentukan learn_radius dan learn_ratio pada setiap iterasi. Perlu diperhatikan bahwa nilai dari learn_radius dan learn_ratio pada setiap interasi akan semakin berkurang. Saya akan menjelaskan secara terpisah proses melakukan perhitungan learn_radius dan learn_ratio.
Menentukan learn_radius
Setelah proses menentukan BMU, tahap selanjutnya adalah menentukan neighbourhood dari BMU. Pada SOM proses updating nilai weight pada network hanya akan dilakukan terhadap neuron yang berada dalam radius neighbourhood BMU.
 |
|---|
| Ilustrasi learning radius |
Dalam SOM radius neighborhood akan menyusut pada setiap ilustrasi, pada ilustrasi diatas dapat dilihat bahwa radius neighborhood pada iterasi pertama (gambar sebelah kiri) lebih besar dibandingkan radius neighbourhood pada iterasi ke-10 (gambar sebelah kanan). Dalam SOM proses ini dilakukan dengan menerapkan fungsi Exponential decay.
\[ \sigma = \sigma_0 * e ^ (\frac{-t}{k})\]dimana
\[\sigma_0 = max (widthTP, heightTP) / 2\] \[k = \frac{numInput}{log(\sigma_0)}\]Sedangkan proses untuk menentukan radius neighbourhood dari BMU pada topographic maps dapat digunakan formula
\[learn\_radius = exp ^ {(\frac{-S^2}{2\sigma^2})}\]dimana
\[S = \| tp - BMU \|\]Keterangan:
- tp = topographic maps
- widthTP = lebar topographic maps
- heightTP = tinggi topographic maps
- numInput = jumlah training data
- || a - b || = euclidian distance point a dan point b
Implementasi pada python
S = np.linalg.norm(self.tp - bmu, axis=1)
sigma = self.dMapRadius * exp(-t/self.k)
learn_radius = np.exp(- ((S ** 2) / (2 * sigma ** 2)))
Penjelasan:
- np.linalg.norm(self.tp - bmu, axis=1) = menghitung euclidian distance antara BMU dan setiap point pada topograhic maps
- axis = 1, peritungan dilakukan sepanjang axis pertama dalam kasus ini row
a = np.matrix([[1, 2 ], [3, 4]])
b = np.matrix([[1, 2 ]])
np.linalg.norm(a - b, axis = 1) = array([ 0., 2.82842712])
- S ** 2 = \(S ^ 2\)
- np.exp() = fungsi untuk menghitung nilai exponential
- t = ith iterasi, pada iterasi pertama t = 1, sedangkan pada iterasi ke 10 t = 10
Menentukan learn_ratio
Sama halnya dengan learn_radius, nilai dari learn ratio akan menyusut pada setiap iterasi. Untuk menghitung nilai dari learn_ratio digunakan formula
\[learn\_ratio = \lambda * exp {(\frac{-t}{k})}\]Keterangan:
\(\lambda\) = learning rate (constanta) Implementasi pada python
learn_ratio = self.learningRate * exp(-t/self.k)
Setelah melakukan proses perhitungan nilai learn_radius dan learn_rate, maka proses updating weight neuron dapat dilakukan dengan menggunakan formula
\[w(t + 1) = \Delta w + w(t)\]dimana
\[\Delta w = learn_ratio * learn_radius * (x - w)\]Keterangan:
- x = sample dari trainind data
- w = weight neuron
Implementasi pada python
self.w += learn_ratio * learn_radius[:, np.newaxis] * (x - self.w)
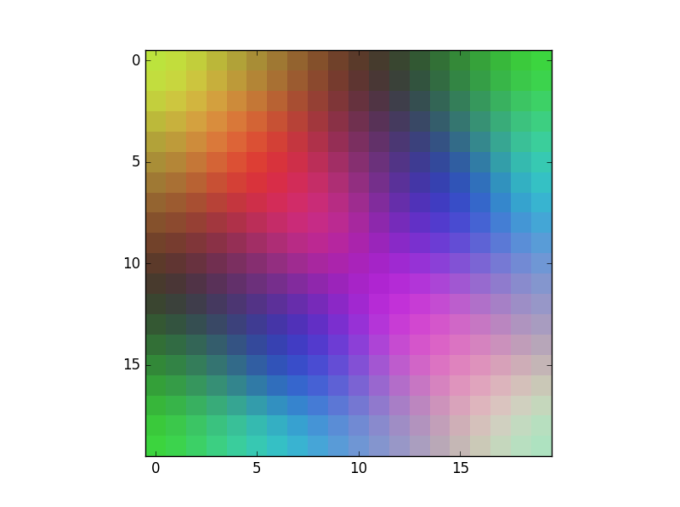
Dalam implementasi pada python saya tidak melakukan proses random dalam pemilihan sample, akan tetapi setiap sample akan diambil secara berurutan pada setiap iterasi. Dalam implemntasi ini, saya menggunakan SOM untuk melakukan clustering warna.
 |
|---|
| Weight neuron sebelum proses training |
 |
|---|
| Weight neuron setelah proses learning |
Untuk code implementasi selengkapnya bisa